OpenCV solvePnP: Get Camera Position in World Coordinates

• Introduction
• Step-by-Step Guide
• Code Example
• Additional Notes
• Summary
• Conclusion
• References

In computer vision, determining the position and orientation of a camera from a single image, known as camera pose estimation, is a fundamental problem. This process involves understanding how a 3D scene is projected onto a 2D image plane. This article provides a step-by-step guide on how to perform camera pose estimation using OpenCV in Python. We will cover camera calibration, establishing 3D-2D point correspondences, utilizing the solvePnP function, and interpreting the results to obtain the camera's position and orientation in the world coordinate system.

1. Calibrate your camera: Obtain the intrinsic matrix (focal length, principal point) and distortion coefficients.

   ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1], None, None)

2. Identify 3D-2D point correspondences: You need a set of 3D points in the world coordinate system and their corresponding 2D projections in the image.

   # 3D points in world coordinates
   world_points = np.array([[0, 0, 0], [1, 0, 0], [0, 1, 0]], dtype=np.float32)
   
   # Corresponding 2D points in image coordinates
   image_points = np.array([[100, 100], [200, 100], [100, 200]], dtype=np.float32)

3. Use cv2.solvePnP(): This function estimates the camera pose (rotation and translation) from the 3D-2D point correspondences.

   success, rotation_vector, translation_vector = cv2.solvePnP(world_points, image_points, mtx, dist)

4. Convert rotation vector to rotation matrix:

   rotation_matrix, _ = cv2.Rodrigues(rotation_vector)

5. Camera position: The translation vector from solvePnP represents the camera's position in the world coordinate system.

6. Camera orientation: The rotation matrix represents the camera's orientation in the world coordinate system.

Note:

• Ensure the 3D and 2D points are correctly paired.
• The accuracy of the pose estimation depends on the accuracy of camera calibration and point correspondences.
• The coordinate systems used in OpenCV can be confusing. Make sure you understand the conventions used.

This Python code estimates the position and orientation of a calibrated camera using 3D-2D point correspondences. It assumes pre-calibrated camera parameters and takes known 3D points and their corresponding 2D projections in an image. The code utilizes OpenCV's solvePnP function to compute the camera pose, represented by a rotation and translation vector. The rotation vector is then converted to a rotation matrix for easier interpretation. Finally, the code calculates and displays the camera's position and orientation.

import cv2
import numpy as np

# Placeholder for image and object points from calibration
# (Replace with actual values from your calibration)
objpoints = ... 
imgpoints = ...

# Camera calibration
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1], None, None)

# 3D points in world coordinates (example)
world_points = np.array([[0, 0, 0], [1, 0, 0], [0, 1, 0]], dtype=np.float32)

# Corresponding 2D points in image coordinates (example)
image_points = np.array([[100, 100], [200, 100], [100, 200]], dtype=np.float32)

# Estimate camera pose
success, rotation_vector, translation_vector = cv2.solvePnP(world_points, image_points, mtx, dist)

# Convert rotation vector to rotation matrix
rotation_matrix, _ = cv2.Rodrigues(rotation_vector)

# Camera position
camera_position = -np.dot(rotation_matrix.T, translation_vector)

# Print results
print("Camera Position:\n", camera_position)
print("Camera Orientation (Rotation Matrix):\n", rotation_matrix)

# Further actions:
# - Project 3D points to the image plane using cv2.projectPoints()
# - Visualize the camera pose in 3D space

Explanation:

1. Calibration: This code assumes you have already calibrated your camera and obtained mtx (intrinsic matrix) and dist (distortion coefficients).
2. Point Correspondences: Replace the example world_points and image_points with your actual 3D-2D point pairs.
3. Pose Estimation: cv2.solvePnP() calculates the rotation_vector and translation_vector representing the camera pose.
4. Rotation Matrix: The rotation vector is converted to a more interpretable rotation matrix using cv2.Rodrigues().
5. Camera Position and Orientation: The translation_vector directly represents the camera position. The rotation_matrix describes the camera's orientation in the world coordinate system.

Important:

• Coordinate Systems: Understand the coordinate systems used for your 3D points, 2D points, and camera pose. OpenCV's conventions might differ from other libraries or datasets.
• Accuracy: The accuracy of pose estimation heavily relies on accurate camera calibration and precise 3D-2D point correspondences.
• Visualization: Consider using libraries like matplotlib or Open3D to visualize the estimated camera pose and 3D points for better understanding.

• Camera calibration is crucial: The accuracy of the pose estimation heavily depends on the accuracy of the camera calibration. Ensure that the calibration process is performed carefully using a well-defined calibration pattern and capturing images from various angles and distances.
• objpoints and imgpoints: These variables represent the object points and image points, respectively, obtained during camera calibration. These points are essential for estimating the camera's intrinsic parameters.
• Understanding the coordinate systems is key: OpenCV uses a specific coordinate system convention. It's essential to understand the relationship between the world coordinate system, camera coordinate system, and image coordinate system to interpret the results correctly.
• The code assumes distortion correction: The mtx and dist parameters obtained from calibration are used in cv2.solvePnP() to correct for lens distortion. If your application requires, you can disable this correction by passing None for the dist argument.
• More than four points are recommended: While cv2.solvePnP() can work with a minimum of four 3D-2D point correspondences, using more points generally improves the accuracy and robustness of the pose estimation.
• Error handling: The success flag returned by cv2.solvePnP() indicates whether the pose estimation was successful. It's good practice to check this flag and handle cases where the estimation fails.
• Real-world applications: Camera pose estimation has numerous applications, including augmented reality, robotics, 3D modeling, and object tracking.
• Alternatives to solvePnP: OpenCV provides other functions for pose estimation, such as cv2.findHomography and cv2.solvePnPRansac. These functions might be more suitable depending on the specific requirements of your application.
• Iterative refinement: The pose estimation can be further refined using iterative optimization techniques like bundle adjustment, which minimizes the reprojection error between the observed and projected 3D points.
• Visualizing the results: Visualizing the estimated camera pose and the 3D points in the image can help verify the accuracy of the estimation and debug any issues. Libraries like matplotlib or Open3D can be used for this purpose.
• The provided code snippet is a starting point: You can extend it further by adding features like drawing the camera pose axes on the image, projecting 3D points onto the image plane, or integrating it into a larger computer vision pipeline.

This guide outlines the process of estimating a camera's position and orientation in 3D space using OpenCV in Python.

Steps:

1. Camera Calibration: Determine the camera's intrinsic parameters (focal length, principal point, distortion coefficients) using cv2.calibrateCamera(). This step requires a set of images with known calibration patterns.

2. Establish 3D-2D Point Correspondences: Identify a set of 3D points in the world coordinate system and their corresponding 2D projections in the image. These points act as anchors for pose estimation.

3. Solve for Camera Pose: Utilize cv2.solvePnP() to estimate the camera's rotation and translation vectors based on the 3D-2D point correspondences, intrinsic matrix, and distortion coefficients.

4. Convert Rotation Vector: Transform the rotation vector obtained from solvePnP() into a more interpretable rotation matrix using cv2.Rodrigues().

5. Interpret Results:

   • Camera Position: The translation vector from solvePnP() directly represents the camera's 3D position in the world coordinate system.
   • Camera Orientation: The rotation matrix describes the camera's 3D orientation relative to the world coordinate system.

Key Considerations:

• Accurate camera calibration and precise 3D-2D point correspondences are crucial for reliable pose estimation.
• Ensure a clear understanding of the coordinate systems used in OpenCV to avoid misinterpretations.

This approach provides a practical method for determining camera pose, enabling applications like augmented reality, 3D reconstruction, and robotics navigation.

By accurately calibrating the camera, establishing precise 3D-2D point correspondences, and employing the robust solvePnP algorithm, we can effectively determine the camera's pose, represented by its position and orientation, from a single image. This fundamental computer vision technique finds wide-ranging applications in fields such as augmented reality, robotics, 3D modeling, and object tracking, enabling interactions between the virtual and real worlds. Understanding the underlying principles, coordinate systems, and potential sources of error is crucial for successful implementation and accurate pose estimation. As computer vision continues to advance, camera pose estimation will undoubtedly play an increasingly vital role in shaping our technological landscape.

• Obtain Camera Pose and camera real world position using ... | Aug 3, 2017 ... Obtain Camera Pose and camera real world position using SolvePnP C++ ... It's a fisheye camera, did you calibrate using the cv::fisheye::calibrate ...
• Python Opencv SolvePnP yields wrong translation vector - Stack ... | Jan 25, 2013 ... Camera position in world coordinate from cv::solvePnP · 24 · How does one convert world coordinates to camera coordinates? 17 · Calculate camera ...
• SolvePNP and world relative rotation - OpenCV | Hello. I am using SolvePNP and rotation is (seems for me) to be relative to camera “look at” orientation instead of camera axis, which are fixed to the world. So for example in order to make sure that rotation is 0 I need look directly with my object to the camera. While I’d like to have angle to be absolute. Can you pls explain how I can get rotation relative to camera axis? Thanks, Greg
• SolvePnP seems......sensitive - Programming - Chief Delphi | It’s the off season, and we’re trying to get things done that didn’t happen during the regular season. High on my list is improving autonomous programming and computer vision. We’re using OpenCV on a Jevois camera. My main task right now is to use the vision targets to guide the robot to the right spot to place hatch panels. Fairly straightforward. Lots of teams have done it, and yet we didn’t get it done this season. There are a few ways to approach this task, but here’s the one I chose: ...
• Camera position in world coordinate from cv::solvePnP ... | The term \
• Finding camera location with solvePNP - Programming - Chief Delphi | We’re trying to get some of the vision tracking going that never quite worked during the season.$@# I’m having a bit of a problem with localization.$@# I’m wondering if anyone in the CD community can spot the flaw in what I am doing. I’m afraid this will be directed mostly to mentors here, but if a student happened to understand the question and provide an answer, I would be very pleased and impressed. $@# My goal is to find the position of the camera in world (model) coordinates by finding th...
• OpenCV solvePnP function outputs (rvec, tvec) : r/computervision | Posted by u/zuliani19 - 3 votes and 4 comments
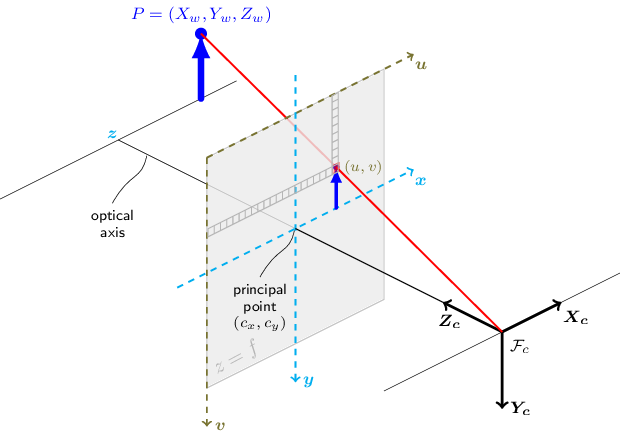• Camera Calibration and 3D Reconstruction - OpenCV | Compute undistorted image points position. void, cv::undistortPoints ... points given in the world's coordinate system into the first image. projMatr2 ...
• Airsim Coordinate Transform/SolvePnP Question · Issue #3577 ... | Question What's your question? Hi, I have two questions: I am confused about the result of Airsim set Pose I have doubts about solvePnP to estimate camera pose I have looked at the issues and could...