Draw a Sparkling Crystal Ball: Two-Color Particle Tutorial
Learn to draw a mesmerizing crystal ball with this step-by-step tutorial, using a two-color particle effect to create a magical and mystical feel.
Learn to draw a mesmerizing crystal ball with this step-by-step tutorial, using a two-color particle effect to create a magical and mystical feel.
This snippet demonstrates how to generate and visualize points uniformly distributed on the surface of a sphere using R. We'll employ spherical coordinates for point generation and then convert them to Cartesian coordinates for visualization with the 'rgl' package.
Generate spherical coordinates:
phi <- runif(100, 0, pi)
theta <- runif(100, 0, 2*pi)Convert to Cartesian coordinates:
x <- sin(phi) * cos(theta)
y <- sin(phi) * sin(theta)
z <- cos(phi)Plot the points on a sphere:
library(rgl)
spheres3d(x, y, z, radius = 0.05)The code generates 100 random points in spherical coordinates, converts them to Cartesian coordinates, and then plots these points as small blue spheres on a 3D sphere using the rgl package in R.
# Generate spherical coordinates
phi <- runif(100, 0, pi)
theta <- runif(100, 0, 2*pi)
# Convert to Cartesian coordinates
x <- sin(phi) * cos(theta)
y <- sin(phi) * sin(theta)
z <- cos(phi)
# Plot the points on a sphere
library(rgl)
spheres3d(x, y, z, radius = 0.05, color = "blue")Explanation:
Generating Spherical Coordinates:
phi: Represents the polar angle (from the positive z-axis) and ranges from 0 to pi.theta: Represents the azimuthal angle (from the positive x-axis) and ranges from 0 to 2*pi.runif(100, 0, pi) generates 100 random values between 0 and pi for phi.runif(100, 0, 2*pi) generates 100 random values between 0 and 2*pi for theta.Converting to Cartesian Coordinates:
Plotting the Points:
library(rgl) loads the rgl package for 3D plotting.spheres3d(x, y, z, radius = 0.05, color = "blue") creates a 3D plot with small spheres (radius 0.05) at the calculated (x, y, z) coordinates, representing points on the sphere. The spheres are colored blue.This code will generate a 3D plot of a sphere with 100 randomly distributed points on its surface. You can interact with the plot by rotating, zooming, and panning to view the points from different angles.
Uniform Distribution: The runif() function ensures that the generated points are uniformly distributed on the sphere's surface. This is crucial for applications requiring random sampling on a sphere, such as simulations or Monte Carlo methods.
Alternative Visualization: Instead of spheres3d(), you can use plot3d(x, y, z, type = "p", size = 3, col = "blue") for a simpler point-based visualization.
Sphere Parameters: The code assumes a unit sphere (radius = 1). You can easily adjust the sphere's radius by multiplying the x, y, and z coordinates by the desired radius.
Color Customization: The color argument in spheres3d() can accept a vector of colors, allowing you to assign different colors to each point based on some criteria.
Applications: This code snippet has applications in various fields, including:
Further Exploration:
rgl package for more advanced visualizations.| Step | Description | R Code |
|---|---|---|
| 1 | Generate 100 random spherical coordinates (φ, θ) uniformly distributed over a unit sphere. |
phi <- runif(100, 0, pi)theta <- runif(100, 0, 2*pi)
|
| 2 | Convert the spherical coordinates to Cartesian coordinates (x, y, z). |
x <- sin(phi) * cos(theta)y <- sin(phi) * sin(theta)z <- cos(phi)
|
| 3 | Plot the points on a 3D sphere using the rgl package. Each point is represented as a small sphere with radius 0.05. |
library(rgl)spheres3d(x, y, z, radius = 0.05)
|
Summary: This R code generates 100 random points uniformly distributed on the surface of a unit sphere. It first generates spherical coordinates, then converts them to Cartesian coordinates, and finally visualizes the points in a 3D plot.
This code provides a practical illustration of generating and visualizing uniformly distributed points on a sphere's surface using R. By leveraging spherical coordinates and conversion to Cartesian coordinates, the process is simplified, enabling clear visualization with the 'rgl' package. This technique holds value in diverse fields, including computer graphics, simulations, and geospatial analysis, demonstrating its versatility for tasks requiring random point distribution on a spherical surface.
 Weird Simple Syrup with stringy particles, ok to use? Approx 3 ... | Posted by u/According_Strength98 - 105 votes and 136 comments
Weird Simple Syrup with stringy particles, ok to use? Approx 3 ... | Posted by u/According_Strength98 - 105 votes and 136 comments Segmentation and analysis of spherical caps on spherical particles ... | Hello, I have (many) SEM images of spherical glass nanoparticles with metal spherical caps on them (see example images attached). In a nutshell I would like to determine through image analysis: the fraction of all spherical glass particles possessing a cap for each spherical glass particle having a cap the cap coverage I am very familiar with the basic fiji/imagej functions of filtering, thresholding and particle analysis (we use them a lot to analyse “bare” particles like the pure spherical ...
Segmentation and analysis of spherical caps on spherical particles ... | Hello, I have (many) SEM images of spherical glass nanoparticles with metal spherical caps on them (see example images attached). In a nutshell I would like to determine through image analysis: the fraction of all spherical glass particles possessing a cap for each spherical glass particle having a cap the cap coverage I am very familiar with the basic fiji/imagej functions of filtering, thresholding and particle analysis (we use them a lot to analyse “bare” particles like the pure spherical ...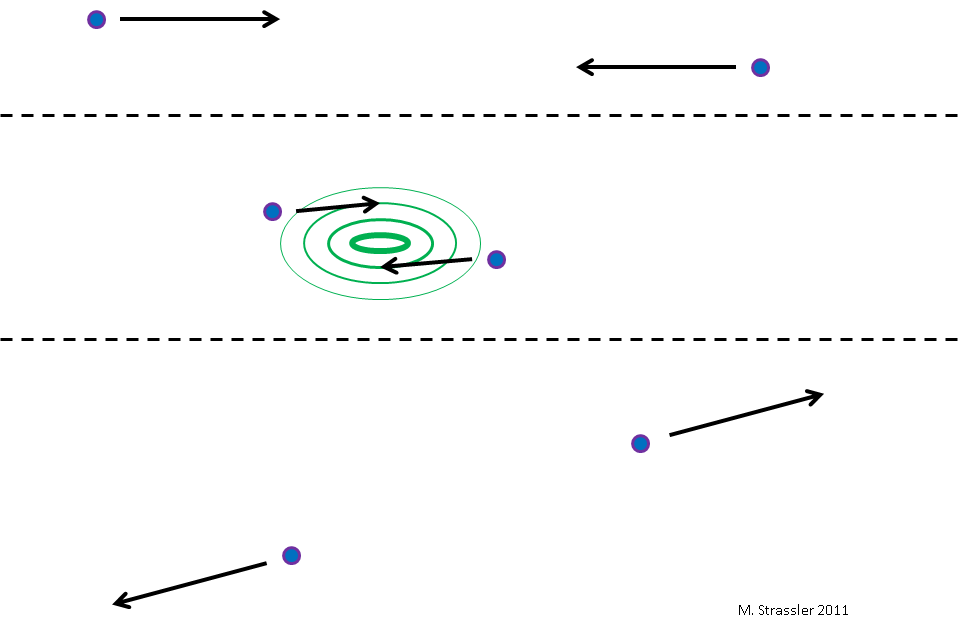 Virtual Particles: What are they? – Of Particular Significance | [For other articles of mine on this subject, focusing on particular topics, see here, here, here or here] The term “virtual particle” is an endlessly confusing and confused subject for …
Virtual Particles: What are they? – Of Particular Significance | [For other articles of mine on this subject, focusing on particular topics, see here, here, here or here] The term “virtual particle” is an endlessly confusing and confused subject for … Particle Accelerator Demo : 4 Steps (with Pictures) - Instructables | Particle Accelerator Demo: A while ago I decide to try to make a simple demo of particle accelerator, and I finally managed to do it. In this Instructable I will show you step by step how to make it.
Particle Accelerator Demo : 4 Steps (with Pictures) - Instructables | Particle Accelerator Demo: A while ago I decide to try to make a simple demo of particle accelerator, and I finally managed to do it. In this Instructable I will show you step by step how to make it.Before we start, let me explain briefly how particle accelerators work and …
 My Crystal Looks Different ~ What Does it Mean when your Crystal ... | crystal change color
My Crystal Looks Different ~ What Does it Mean when your Crystal ... | crystal change color