TensorFlow Regularization: L1, L2 & Dropout Tutorial

• Introduction
• Step-by-Step Guide
• Code Example
• Additional Notes
• Summary
• Conclusion
• References

Regularization techniques are essential for preventing overfitting in neural networks, thereby improving their ability to generalize well to unseen data. This article provides a concise guide on implementing different regularization methods in TensorFlow/Keras, a popular deep learning framework. We will cover L1, L2, and dropout regularization, illustrating how to incorporate them into your neural network models.

1. Import necessary libraries:

   from tensorflow.keras import layers, regularizers

2. Define the regularization strength:

   l2_strength = 0.01  # Adjust this value as needed

3. Add L2 regularization to a layer:

   model.add(layers.Dense(64, 
                          kernel_regularizer=regularizers.l2(l2_strength),
                          activation='relu'))

4. Alternatively, use L1 regularization:

   model.add(layers.Dense(64, 
                          kernel_regularizer=regularizers.l1(l2_strength),
                          activation='relu'))

5. For dropout regularization, add a Dropout layer:

   model.add(layers.Dropout(0.5))  # 0.5 dropout rate

6. Compile and train your model as usual. The regularization penalty will be added to the loss function during training.

This Python code defines a simple sequential neural network using TensorFlow and Keras. It demonstrates how to apply L1, L2, and dropout regularization techniques to the model's layers to prevent overfitting. The code includes adding dense layers with ReLU activation, a dropout layer, and an output layer with softmax activation. It also shows how to compile the model with an optimizer, loss function, and metrics, although the actual training process is commented out. The code provides a basic example of building and regularizing a neural network for classification tasks.

import tensorflow as tf
from tensorflow.keras import layers, regularizers

# Define the regularization strength
l2_strength = 0.01

# Create a simple model
model = tf.keras.Sequential()

# Add a Dense layer with L2 regularization
model.add(layers.Dense(64, 
                        kernel_regularizer=regularizers.l2(l2_strength),
                        activation='relu',
                        input_shape=(10,)))  # Assuming input shape (10,)

# Add another Dense layer with L1 regularization
model.add(layers.Dense(32, 
                        kernel_regularizer=regularizers.l1(l2_strength),
                        activation='relu'))

# Add a Dropout layer for dropout regularization
model.add(layers.Dropout(0.5))

# Add the output layer
model.add(layers.Dense(10, activation='softmax'))

# Compile the model
model.compile(optimizer='adam',
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

# Print the model summary to see the regularization applied
model.summary()

# Prepare your data (replace with your own dataset)
# ...

# Train the model
# model.fit(x_train, y_train, epochs=10, validation_data=(x_val, y_val))

Explanation:

1. Import necessary libraries: This line imports the required classes for building the model and applying regularization.
2. Define regularization strength: This line sets the strength of the L2 regularization. You can adjust this value to control the amount of regularization applied.
3. Add L2 regularization to a layer: This code snippet adds a Dense layer with L2 regularization applied to the kernel weights. The kernel_regularizer argument specifies the regularization technique to use.
4. Alternatively, use L1 regularization: This code snippet demonstrates how to use L1 regularization instead of L2.
5. For dropout regularization: This line adds a Dropout layer with a dropout rate of 0.5. This means that 50% of the neurons will be randomly dropped out during each training epoch.
6. Compile and train: The code then compiles the model with an optimizer, loss function, and metrics. Finally, you would train the model with your data (commented out in the example).

Key points:

• Regularization helps prevent overfitting by adding a penalty to the loss function based on the complexity of the model.
• L1 regularization encourages sparsity in the weights, potentially leading to feature selection.
• L2 regularization encourages small weights for all features.
• Dropout regularization helps prevent co-adaptation of neurons by randomly dropping them out during training.
• You can adjust the regularization strength and dropout rate to find the optimal values for your specific problem.

General:

• Purpose: The primary goal of regularization is to prevent overfitting, which occurs when a model learns the training data too well and fails to generalize to unseen data.
• Balancing Act: Finding the right amount of regularization is crucial. Too little regularization might not prevent overfitting, while too much can lead to underfitting, where the model is too simple to capture the underlying patterns in the data.
• Hyperparameter Tuning: The regularization strength (e.g., l2_strength) and dropout rate are hyperparameters that need to be tuned to find the optimal values for your specific dataset and model architecture. Techniques like cross-validation can be used for this purpose.

L1 and L2 Regularization:

• Weight Penalty: Both L1 and L2 regularization work by adding a penalty term to the loss function. This penalty is proportional to the magnitude of the weights in the network.
• L1 vs. L2:
  • L1 regularization (Lasso) forces the weights of uninformative features to be exactly zero, effectively performing feature selection.
  • L2 regularization (Ridge) keeps all the weights small but non-zero, preventing any single feature from dominating the model.

Dropout Regularization:

• Mechanism: During each training step, dropout randomly "turns off" a fraction of neurons in the layer. This prevents neurons from co-adapting too much and forces the network to learn more robust features.
• Application: Dropout is typically applied to the hidden layers of a neural network.
• Inference: During inference (making predictions), dropout is turned off, and all neurons are used.

Code Example Enhancements:

• Data Loading and Preprocessing: The example code omits data loading and preprocessing steps. In a real-world scenario, you would need to load your dataset, split it into training and validation sets, and perform any necessary preprocessing (e.g., normalization, one-hot encoding).
• Model Evaluation: After training, it's essential to evaluate the model's performance on a separate test set to get an unbiased estimate of its generalization ability.
• Visualization: Plotting the training and validation loss curves can help diagnose overfitting and assess the effectiveness of the regularization techniques.

Beyond the Basics:

• Other Regularization Techniques: There are other regularization methods available in TensorFlow/Keras, such as early stopping and weight constraints.
• Regularization in Different Layers: You can apply regularization to different layers in your network, not just Dense layers. For example, you can use kernel regularization in convolutional layers.
• Custom Regularizers: TensorFlow/Keras allows you to define your own custom regularization functions for more specialized use cases.

This code snippet demonstrates how to implement different regularization techniques in TensorFlow/Keras to prevent overfitting in neural networks:

1. L2 Regularization:

• Purpose: Penalizes large weights in the model by adding the sum of squared weights multiplied by a regularization strength (l2_strength) to the loss function. This encourages the model to learn smaller, more generalized weights.
• Implementation: Use kernel_regularizer=regularizers.l2(l2_strength) within a layer definition.

2. L1 Regularization:

• Purpose: Similar to L2 regularization, but penalizes the sum of absolute weights instead of squared weights. This can lead to sparser weight matrices with many weights being zero.
• Implementation: Use kernel_regularizer=regularizers.l1(l2_strength) within a layer definition.

3. Dropout Regularization:

• Purpose: Randomly drops out a proportion of neurons during each training step, forcing the network to learn more robust features that are not reliant on any single neuron.
• Implementation: Add a layers.Dropout(rate) layer after the layer you want to apply dropout to. rate represents the dropout rate (e.g., 0.5 for dropping 50% of neurons).

General Notes:

• The regularization strength (l2_strength) controls the impact of the regularization penalty. Higher values lead to stronger regularization.
• You can apply these regularization techniques to any layer in your model.
• Regularization is typically applied during training and not during inference.

By applying these techniques and carefully tuning their parameters, you can enhance the generalization ability of your models, making them more robust and reliable for real-world applications. Remember that the choice of regularization techniques and their strength often depends on the specific dataset and model architecture, so experimentation and validation are crucial for finding the optimal settings. This article provides a foundational understanding of regularization in TensorFlow/Keras, empowering you to build more robust and generalizable neural networks.

• tf.keras.Regularizer | TensorFlow v2.16.1 | Regularizer base class.
• Regularization in TensorFlow using Keras API | by Robert Thas John | Regularization is a technique for preventing over-fitting by penalizing a model for having large weights. There are two popular…
• tf.keras.regularizers.L2 | TensorFlow v2.16.1 | A regularizer that applies a L2 regularization penalty.
• 4 ways to improve your TensorFlow model – key regularization ... | Regularization techniques are crucial for preventing your models from overfitting and enables them perform better on your validation and test sets. This guide provides a thorough overview with code of four key approaches you can use for regularization in TensorFlow.
• Applying L2 Regularization to All Weights in TensorFlow ... | A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions.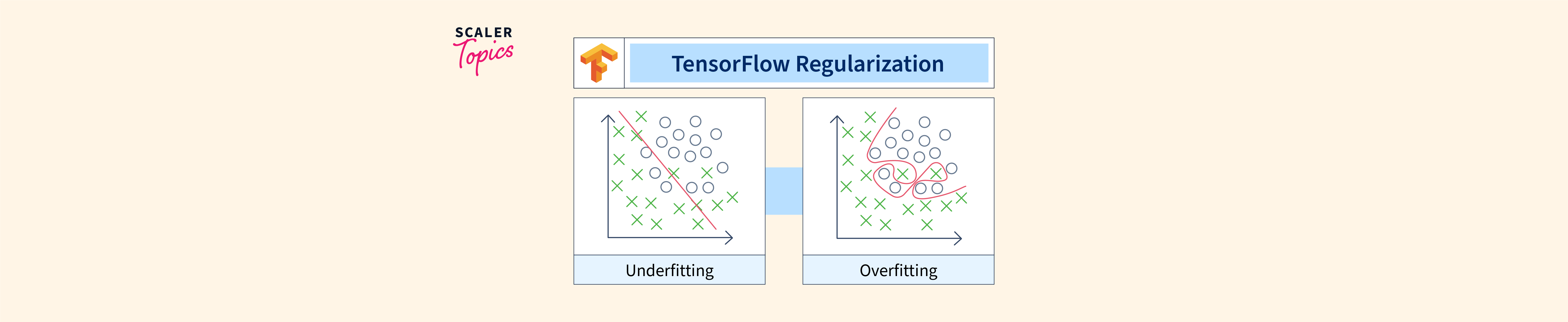
• TensorFlow Regularization - Scaler Topics | This tutorial covers the concept of regularization in machine learning and how to implement L1 and L2 regularization using TensorFlow. Learn how to improve your models by preventing overfitting and tuning regularization strength.
• Convolutional Neural Network and Regularization Techniques with ... | This GIF shows how neural network “learns” from its input. We don’t want the neural network pick up unwanted patterns nor do we want the…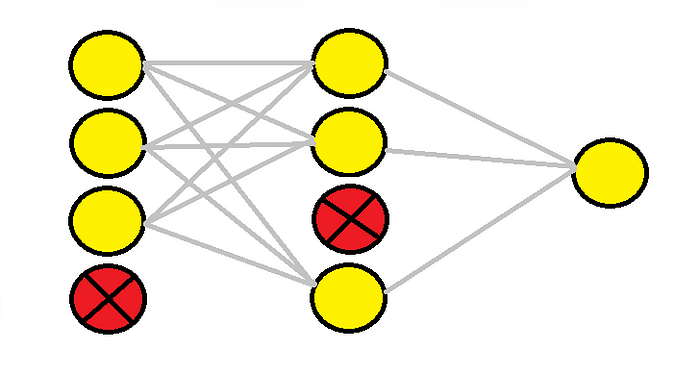
• Dropout Regularization With Tensorflow Keras - Comet | Deep neural networks are complex models which makes them much more prone to overfitting — especially when the dataset has few examples. Left unhandled, an overfit model would fail to generalize well to unseen instances.
• How to Add Regularization to Keras Pre-trained Models the Right ... | Nov 26, 2019 ... How to Add Regularization to Keras Pre-trained Models the Right Way. [ machine-learning deep-learning regularization tensorflow keras ].