Calculating CNN Parameters: A Simple Guide

• Introduction
• Step-by-Step Guide
• Code Example
• Additional Notes
• Summary
• Conclusion
• References

Understanding the number of parameters in a convolutional neural network (CNN) is crucial for comprehending its complexity and potential for learning. This guide provides a step-by-step approach to calculate the parameter count in a convolutional layer.

To calculate the number of parameters in a convolutional layer, follow these steps:

1. Identify key variables:

   • k: Number of filters (or kernels)
   • f: Filter size (assuming square filters, e.g., 3x3)
   • c: Number of channels in the input image (e.g., 3 for RGB)

2. Calculate parameters per filter:

   • Multiply the filter size by the number of channels: f * f * c
   • Add 1 for the bias term: (f * f * c) + 1

3. Calculate total parameters:

   • Multiply the parameters per filter by the number of filters: ((f * f * c) + 1) * k

Example:

k = 32  # Number of filters
f = 3   # Filter size (3x3)
c = 3   # Input channels (RGB)

parameters_per_filter = (f * f * c) + 1 
total_parameters = parameters_per_filter * k

print(total_parameters)  # Output: 896

This calculation ensures you account for all the weights and biases within a convolutional layer.

This Python code defines a function to calculate the number of parameters in a convolutional layer of a neural network. It takes the number of filters, filter size, and input channels as input. It calculates and returns the total number of parameters, accounting for weights and biases. An example usage demonstrates the function with specific values for a convolutional layer.

def calculate_conv_layer_params(k, f, c):
  """
  Calculates the number of parameters in a convolutional layer.

  Args:
    k: Number of filters.
    f: Filter size (assuming square filters).
    c: Number of channels in the input image.

  Returns:
    The total number of parameters in the convolutional layer.
  """

  parameters_per_filter = (f * f * c) + 1
  total_parameters = parameters_per_filter * k
  return total_parameters

# Example usage
k = 32  # Number of filters
f = 3   # Filter size (3x3)
c = 3   # Input channels (RGB)

total_parameters = calculate_conv_layer_params(k, f, c)
print(f"Total parameters in the convolutional layer: {total_parameters}") 

Explanation:

1. Function Definition:

   • We define a function calculate_conv_layer_params to encapsulate the calculation logic, making it reusable.
   • The function takes k, f, and c as input arguments.

2. Calculation:

   • Inside the function, we perform the parameter calculation as described in the article.
   • First, we calculate parameters_per_filter.
   • Then, we multiply it by k to get total_parameters.

3. Return Value:

   • The function returns the calculated total_parameters.

4. Example Usage:

   • We demonstrate how to use the function with example values for k, f, and c.
   • The result is printed to the console.

This code provides a clear and reusable way to calculate the number of parameters in a convolutional layer, making it easier to understand and analyze the complexity of your convolutional neural networks.

• Filter Size: While the example assumes square filters (e.g., 3x3), filters can be rectangular (e.g., 5x3). In such cases, calculate the filter size as f_height * f_width instead of f * f.
• Padding and Strides: This calculation doesn't consider padding or strides, which can influence the output size and indirectly affect the number of parameters in subsequent layers.
• Shared Weights: It's important to remember that the parameters within a filter are shared across the entire input image. This weight sharing significantly reduces the total number of parameters compared to a fully connected layer.
• Deeper Networks: In a CNN with multiple convolutional layers, you need to calculate the parameters for each layer separately and sum them up to get the total parameter count for the entire network.
• Other Layers: This calculation only applies to convolutional layers. Other layers like pooling layers and fully connected layers have their own parameter calculations.
• Practical Implications: Understanding the number of parameters helps in:
  • Model Complexity: More parameters generally mean a more complex model with higher capacity but also a greater risk of overfitting.
  • Computational Cost: More parameters require more computational resources for training and inference.
  • Memory Footprint: More parameters lead to a larger memory footprint for storing the model.

Additional Considerations:

• Regularization: Techniques like weight decay (L2 regularization) can impact the effective number of parameters by driving some weights closer to zero.
• Parameter Efficiency: Modern architectures often employ techniques like depthwise separable convolutions or bottleneck layers to reduce the parameter count without sacrificing performance.

Calculation:

1. Parameters per filter: (f * f * c) + 1
2. Total parameters: ((f * f * c) + 1) * k

Explanation:

• Each filter has f * f * c weights (one for each pixel in the filter and input channel) and 1 bias term.
• The total number of parameters is the number of parameters per filter multiplied by the total number of filters.

By understanding how to calculate the number of parameters in a convolutional layer, you gain valuable insights into the complexity and capacity of your CNN models. This knowledge empowers you to make informed decisions regarding architecture choices, regularization techniques, and resource allocation for training and deployment. Remember to consider factors like padding, strides, and weight sharing for a comprehensive understanding of parameter efficiency in your convolutional neural networks.

• How to calculate the number of parameters in CNN? - GeeksforGeeks | A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions.
• Simple Explanation for Calculating the Number of Parameters in ... | Total number of parameters, output shape in the Convolution layer Photo by Yan Krukov from Pexels In this article, we will go through two important concepts in the convolution layer. How to calcula…
• Understanding and Calculating the number of Parameters in ... | If you’ve been playing with CNN’s it is common to encounter a summary of parameters as seen in the above image. We all know it is easy to…
• filters - How to calculate the number of parameters of a convolutional ... | Mar 16, 2020 ... In your case, the number of parameters is 10∗(3∗3∗3)+10=280. A TensorFlow proof. The following simple TensorFlow (version 2) program can confirm ...
• How to calculate the number of parameters in the CNN? | by ... | Every Machine Learning Engineer/Software Developer/Students who interested in Machine Learning have worked on Convolution Neural Network…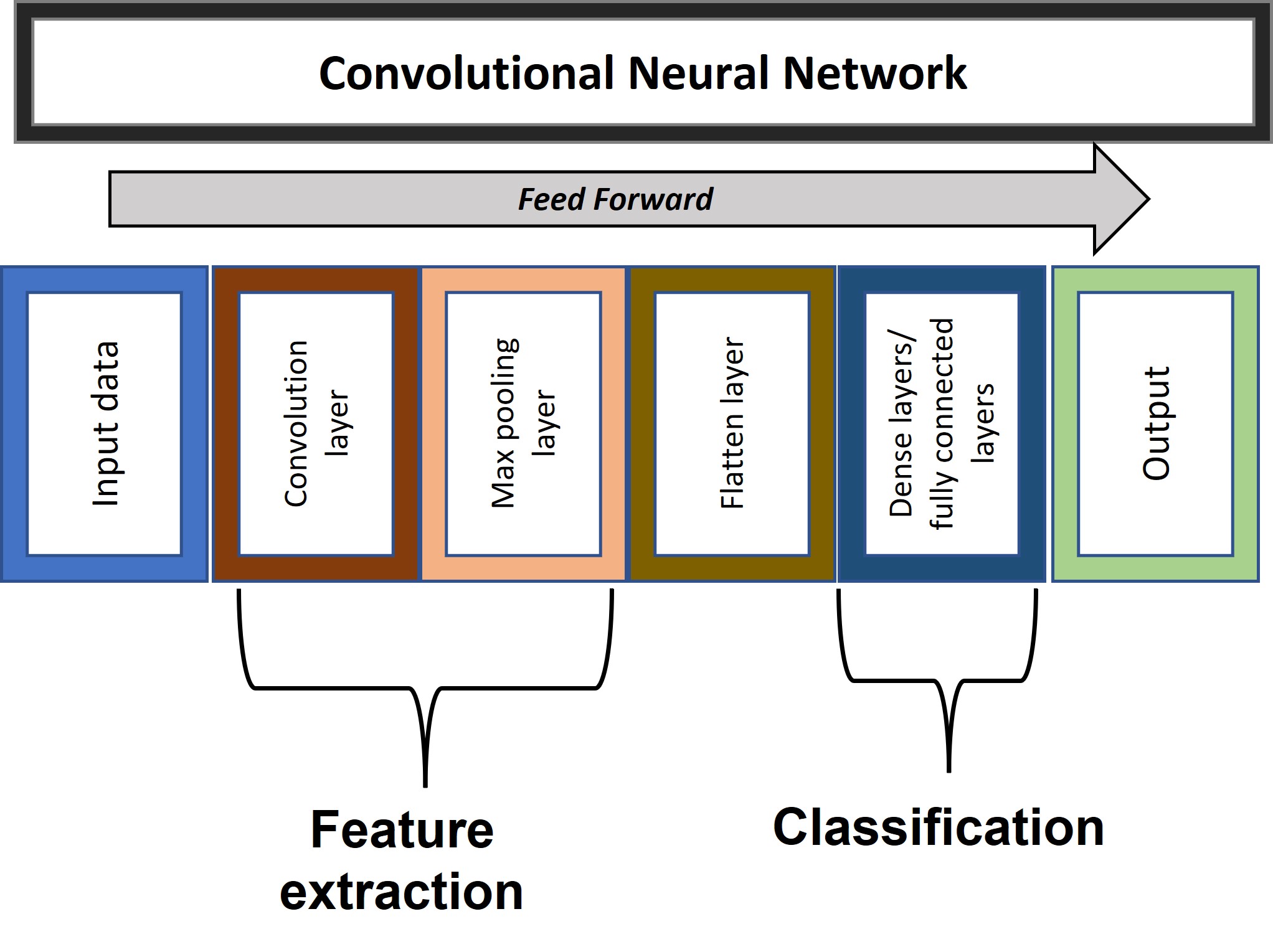
• How to Calculate parameters in Convolutional Neural Network (CNN) | Jun 14, 2023 ... We see there are three columns: layer type, output shape and number of parameters. Before probing deeper into the calculation of parameters, let ...
• Parameter calculation for 2D Convolutions, Calculating total number ... | Generally speaking, the larger the internal structure of a neural network is, the more data points it needs to train. A general-principle…
• Number of Parameters and Tensor Sizes in a Convolutional Neural ... | How to calculate the sizes of tensors (images) and the number of parameters in a layer in a Convolutional Neural Network (CNN). We share formulas with AlexNet as an example.
• machine learning - How many parameters in a Conv2d Layer ... | Jul 10, 2019 ... The right answer is the fourth. From this, the formula to calculate the number of parameters in a convolutional layer is (nml+1)*k with n ...